|
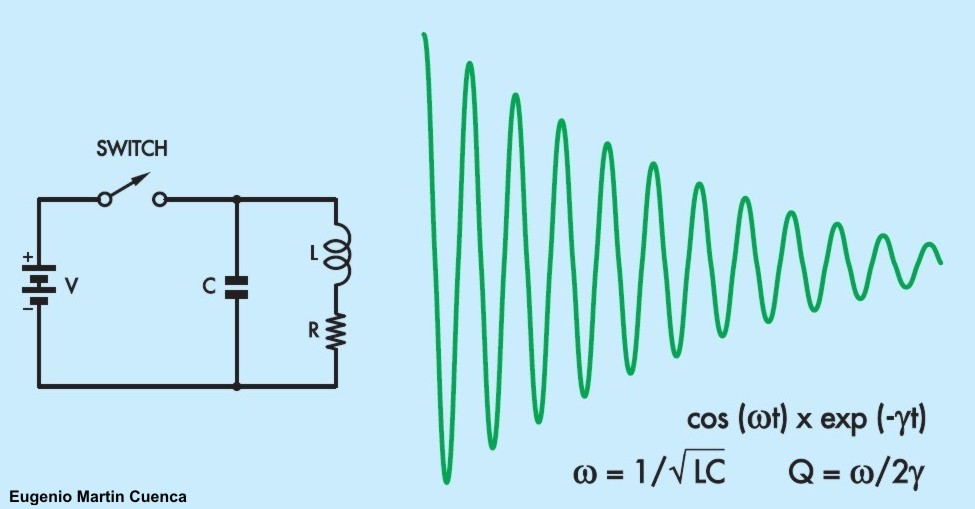
1. 1. - FACTOR DE CALIDAD Q. La resonancia es un fenómeno muy común, especialmente en electrónica, acústica, mecánica y óptica. Cuando se desea una resonancia, se construyen dispositivos especiales, llamados resonadores, con la propiedad de oscilar naturalmente a alguna frecuencia, llamada frecuencia de resonancia, con mucha mayor amplitud que a otras. Todos los resonadores se caracterizan por su frecuencia de resonancia F0 y su factor de calidad Q: Se explica un método simple de medición de Q, el método de anulación. En electrónica, los circuitos LC son un tipo común de resonador, a menudo llamado circuito resonante, circuito sintonizado o circuito tanque. Todos están compuestos por un inductor (L) y un condensador (C) conectados entre sí. La resistencia (R) es responsable de las pérdidas y del factor Q final: A menudo se ignora u omite y rara vez se agrega como un componente físico, pero siempre está presente ya que cualquier pérdida en el resonador aparecerá como una resistencia. Por lo tanto, cada circuito práctico LC es en realidad un circuito RLC. Por lo general, el inductor es responsable de la mayoría de las pérdidas.
El método de anulación se aplica a todo tipo de resonadores, porque las
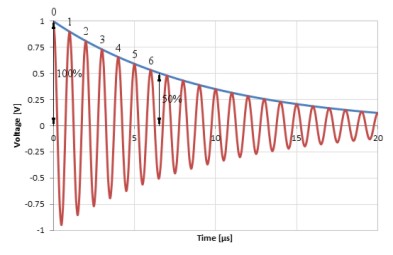
ecuaciones que describen su comportamiento tienen la misma forma. Método de anulación. Es extremadamente simple: primero se "arranca" el resonador de alguna forma para que oscile a su frecuencia natural y luego, observando la disminución de la amplitud de las oscilaciones, se cuentan cuántos ciclos se necesitan para reducir a la mitad la amplitud y se multiplica por 4,53 para calcular Q. En la siguiente gráfica se muestra un ejemplo: La línea roja es la señal del resonador, la línea azul es su envolvente. Por supuesto, no verá la línea de la envolvente en un osciloscopio, pero es bastante fácil imaginarla mirando la señal, ya que la envolvente representa la amplitud de las oscilaciones.
Cuente los períodos hasta que la amplitud se reduzca a la mitad. Aquí Q = 30.
Tomamos la referencia del 100% en t = 0 y vemos que se necesitan
alrededor de 6,5 ciclos para que la amplitud disminuya un 50%.
Simplemente haciendo 6,5 • 4,53 encontramos Q
aproximadamente 30. Este método parece realmente simple, y de hecho lo es, pero debe tener cuidado: lo que está midiendo es el factor Q total del resonador degradado por las pérdidas adicionales introducidas debido al método que se usa para medir la amplitud de la oscilación (el osciloscopio, por ejemplo) y los debidos a la forma en que se "agita" el resonador. El factor Q del resonador siempre será algo mayor. Debe elegirse sabiamente la configuración para minimizar estas pérdidas. Generalmente se traduce en el acoplamiento de los instrumentos de prueba tan sueltos como sea posible al resonador al tiempo que todavía tiene suficiente señal para una medición fiable.
Si no necesita alta precisión, y Q rara vez necesita
ser muy preciso, puede aproximar a 4,53 a 5. Contar algunas
oscilaciones en una pantalla y multiplicar por 5 es algo que puede
hacer rápidamente sin necesidad de
una calculadora.
En mi opinión, esta es la belleza de este método,
puede simplemente observar una forma de onda en su
osciloscopio y "ver" directamente el
factor Q.
1. 2. - EJEMPLOS. Echemos un vistazo a algunos ejemplos para ver cómo funciona este método. Primero tomemos un pequeño inductor de ferrita y lo conectamos en paralelo a un condensador cerámico. El inductor mide 2,56 μH y el condensador 448 pF (la frecuencia de resonancia es por lo tanto 4,700 MHz correspondiente a un período de 213 ns). La configuración de la prueba es visible en la siguiente imagen, donde el bucle se conecta al generador de onda cuadrada y el osciloscopio se conecta en paralelo con el circuito LC con una sonda de voltaje 10: 1. Debido a que el inductor está blindado, el circuito de acoplamiento debe estar bastante cerca del circuito del tanque para poder tener algún acoplamiento. Un pequeño inductor de ferrita de 2,56 μH y un
capacitor cerámico de 448 pF que se comprueba con el método de
anulación. El generador de onda cuadrada está conectado al bucle y el
osciloscopio está en paralelo a través de una sonda 10: 1. Señal de anulación del circuito. 10 mV / DIV, 0,5 μs / DIV. La amplitud de las señales se reduce a la mitad en aproximadamente 2,5 ciclos, el factor Q es por lo tanto 11.3.
El factor Q de este tanque no es muy bueno: 11.4 es bastante bajo, aunque no es sorprendente. Los inductores pequeños como este están destinados principalmente a la conmutación de fuentes de alimentación y generalmente tienen un factor Q entre 10 y 20, solo algunos modelos costosos y raros pueden llegar a 40. El condensador cerámico utilizado aquí es bueno para aplicaciones de alta frecuencia y no (negativamente ) influye en el factor Q. Segundo ejemplo. Hagamos la misma prueba con un inductor mejor. Elija un inductor de núcleo de aire hecho con hilo de cobre grueso L = 2.05 μH (no es exactamente la misma inductancia que antes pero lo suficientemente proxima) y un condensador de cerámica de alto voltaje de 490 pF (la frecuencia de resonancia es 5.022 MHz correspondiente un período de 199 ns). Estos componentes están diseñados para construir transmisores de alta potencia: manejan alta potencia con muy pocas pérdidas. El inductor está compuesto por 8 vueltas de hilo de cobre de Ø8 mm aligerados en un núcleo de aire de Ø62 mm de diámetro interno. El paso de la bobina es de 14 mm. La configuración de la prueba es visible en la siguiente imagen, donde el bucle se conecta al generador de onda cuadrada y el osciloscopio se conecta en paralelo con el circuito LC con una sonda de voltaje 10: 1. La posición del lazo se ha ajustado hasta que se ha logrado el acoplamiento deseado: en este caso, bastante lejos del inductor porque la configuración del núcleo de aire garantiza un acoplamiento mucho mejor que antes.
Un inductor de núcleo de aire de 2.05 μH y un
condensador cerámico de alta tensión de 490 pF que se está probando con
el método de reducción de llamada. El generador de onda cuadrada está
conectado al bucle y el osciloscopio está en paralelo a través de una
sonda 10: 1. Señal de anulación del circuito. 10 mV / DIV, 2 μs / DIV. La amplitud de las señales se reduce a la mitad en aproximadamente 63 ciclos, el factor Q es por lo tanto 285. Como puede ver, la amplitud de la señal disminuye
mucho más lentamente y se reduce a la mitad en aproximadamente 63
ciclos. Podemos calcular fácilmente el factor Q multiplicando por 4,53 y
encontramos Q = 285. Este es un factor de calidad muy bueno: los buenos
inductores son generalmente de alrededor de 250, pero el precio a pagar
es el tamaño más grande y la gran cantidad de cobre precioso (y a veces
de plata) necesarios para construirlos. Solo por diversión, echemos un vistazo a un circuito resonante LC aún mejor: una antena de circuito magnético. El representado en la siguiente imagen está compuesto por 2 vueltas de tubo de cobre de Ø18 mm en un núcleo de aire de Ø95 cm. El paso de la bobina es de 40 mm y mide 7.4 μH. Está sintonizado a 1.850 MHz con un condensador de vacío de 1.0 nF.
|